Big-O Notation
This post is hugely referenced by Big-O Notation Explained with Examples
Asymptotic notation is a set of languages which allow us to express the performance of our algorithms in relation to their input. Big O notation is used in Computer Science to describe the performance or complexity of an algorithm. Big O specifically describes the worst-case scenario, and can be used to describe the execution time required or the space used (e.g. in memory or on disk) by an algorithm.
Big O complexity can be visualized with this graph:
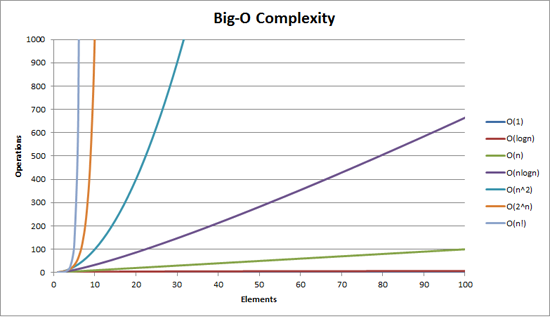
Source: Big-O Notation Explained with Examples
As a programmer first and a mathematician second (or maybe third or last) here the best way to understand Big O thoroughly examples in code. So, below are some common orders of growth along with descriptions and examples where possible.
1. O(1)
void printFirstElementOfArray(int arr[])
{
printf("First element of array = %d",arr[0]);
}
This function runs in O(1) time (or "constant time") relative to its input. The input array could be 1 item or 1,000 items, but this function would still just require one step.
2. O(n)
void printAllElementOfArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%d\n", arr[i]);
}
}
This function runs in O(n) time (or "linear time"), where n is the number of items in the array. If the array has 10 items, we have to print 10 times. If it has 1000 items, we have to print 1000 times.
3. O(n^2)
void printAllPossibleOrderedPairs(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
printf("%d = %d\n", arr[i], arr[j]);
}
}
}
Here we're nesting two loops. If our array has n items, our outer loop runs n times and our inner loop runs n times for each iteration of the outer loop, giving us n2 total prints. Thus this function runs in O(n2) time (or "quadratic time"). If the array has 10 items, we have to print 100 times. If it has 1000 items, we have to print 1000000 times.
4. O(2^n)
int fibonacci(int num)
{
if (num <= 1) return num;
return fibonacci(num - 2) + fibonacci(num - 1);
}
An example of an O(2n) function is the recursive calculation of Fibonacci numbers. O(2n) denotes an algorithm whose growth doubles with each addition to the input data set. The growth curve of an O(2n) function is exponential - starting off very shallow, then rising meteorically.
5. Drop the constants
When you're calculating the big O complexity of something, you just throw out the constants. Like:
void printAllItemsTwice(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%d\n", arr[i]);
}
for (int i = 0; i < size; i++)
{
printf("%d\n", arr[i]);
}
}
This is O(2n), which we just call O(n).
void printFirstItemThenFirstHalfThenSayHi100Times(int arr[], int size)
{
printf("First element of array = %d\n",arr[0]);
for (int i = 0; i < size/2; i++)
{
printf("%d\n", arr[i]);
}
for (int i = 0; i < 100; i++)
{
printf("Hi\n");
}
}
This is O(1 + n/2 + 100), which we just call O(n).
Why can we get away with this? Remember, for big O notation we're looking at what happens as n gets arbitrarily large. As n gets really big, adding 100 or dividing by 2 has a decreasingly significant effect.
6. Drop the less significant terms
void printAllNumbersThenAllPairSums(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%d\n", arr[i]);
}
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
printf("%d\n", arr[i] + arr[j]);
}
}
}
Here our runtime is O(n + n2), which we just call O(n2).
Similarly:
- O(n3 + 50n2 + 10000) is O(n3)
- O((n + 30) * (n + 5)) is O(n2)
Again, we can get away with this because the less significant terms quickly become, well, less significant as n gets big.
7. With Big-O, we're usually talking about the "worst case"
bool arrayContainsElement(int arr[], int size, int element)
{
for (int i = 0; i < size; i++)
{
if (arr[i] == element) return true;
}
return false;
}
Here we might have 100 items in our array, but the first item might be the that element, in this case we would return in just 1 iteration of our loop.
In general we'd say this is O(n) runtime and the "worst case" part would be implied. But to be more specific we could say this is worst case O(n) and best case O(1) runtime. For some algorithms we can also make rigorous statements about the "average case" runtime.