Intro

What is training and testing?

During training, a machine learning model learns patterns and relationships in a given dataset to make predictions or classifications. The model adjusts its internal parameters iteratively to minimize the error or maximize the performance. Once the training is complete, the model is evaluated on a separate test dataset that was not used during training. The test dataset assesses the model's generalization ability by measuring its performance metrics, such as accuracy or error rate. The goal is to ensure that the model can effectively make predictions on new, unseen data and is not overfitting or memorizing the training data.

Evaluation Metrics

Evaluation metrics in machine learning are quantitative measures used to assess the performance and quality of a machine learning model. These metrics provide an objective evaluation of how well the model is performing on a given task.

The choice of evaluation metrics depends on the specific problem and the desired outcome. For classification tasks, metrics such as accuracy, precision, recall, F1 score, and area under the curve (AUC) are commonly used. In regression tasks, metrics like mean squared error (MSE), mean absolute error (MAE), and R-squared (R2) are often utilized. Evaluation metrics help researchers and practitioners understand the strengths and weaknesses of their models, compare different models, and make informed decisions about model selection and performance optimization.

Errors

Overfitting and underfitting

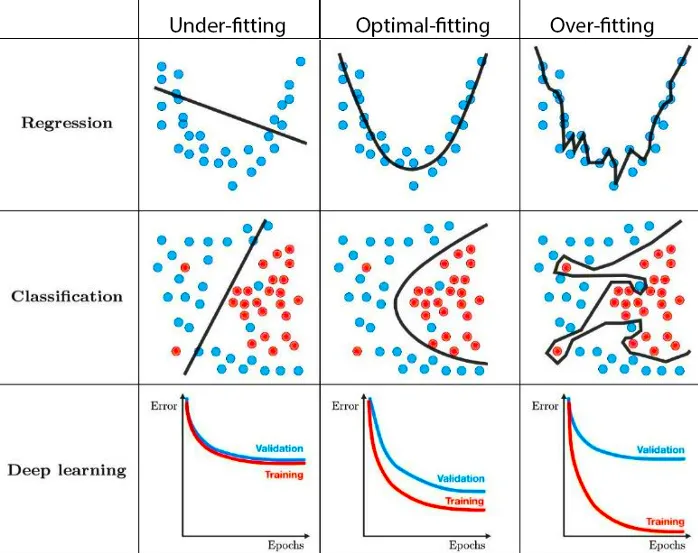
Resource: Techniques for handling underfitting and overfitting in Machine Learning

Overfitting and underfitting are two common phenomena in machine learning that occur when a model is trained on a dataset.

Overfitting/Variance error

Overfitting happens when a model becomes too complex and starts to "memorize" the training data instead of learning the underlying patterns. As a result, the model performs exceptionally well on the training data but fails to generalize to new, unseen data. Overfitting can occur when a model is too flexible or when it is trained on insufficient data. Signs of overfitting include excessively low training error but high testing error or poor performance on new data.

Underfitting/Bias error

Underfitting occurs when a model is too simple or lacks the capacity to capture the complexity of the underlying patterns in the data. In such cases, the model fails to learn the essential relationships and performs poorly both on the training and testing data. Underfitting often indicates that the model is not able to capture the inherent complexity of the problem and may require more sophisticated algorithms or features.

Both overfitting and underfitting are undesirable as they indicate that the model's performance is suboptimal. The goal in machine learning is to strike a balance between these two extremes by selecting an appropriate model complexity, gathering sufficient and diverse training data, and employing techniques like regularization or cross-validation to mitigate the risks of overfitting and underfitting.

Type 1 and Type 2 error

In machine learning, several types of errors can occur during model training and evaluation. Here are some common types of errors:

1. True Positive (TP): The model correctly predicts the positive class.
2. True Negative (TN): The model correctly predicts the negative class.
3. False Positive (FP): The model incorrectly predicts the positive class (Type 1 error).
4. False Negative (FN): The model incorrectly predicts the negative class (Type 2 error).

These four types of errors are the foundation of binary classification evaluation. From these, several performance metrics can be derived, including accuracy, precision, recall (sensitivity), specificity, F1 score, and area under the ROC curve (AUC-ROC).

It's worth noting that the choice of error types and their importance may vary based on the specific problem and the desired outcome. For example, in fraud detection, minimizing false positives (FP) is crucial to avoid wrongly flagging legitimate transactions, while in medical diagnosis, minimizing false negatives (FN) is important to avoid missing potential health risks. Understanding and managing these different error types is essential for effective model evaluation and optimization in machine learning.

Exmpale

Resource: Before we can balance false positives and false negatives, we have to publish false negatives.

Type 1 and Type 2 errors are two types of errors commonly encountered in hypothesis testing and statistical analysis, but they can also be applied to machine learning classification problems.

Type 1 Error (False Positive): Type 1 error occurs when a null hypothesis is incorrectly rejected, indicating a false positive result. In the context of machine learning, it corresponds to incorrectly classifying a negative instance as positive. It is akin to a false positive error discussed earlier. Type 1 errors are particularly relevant when maintaining a low false positive rate is crucial, such as in medical diagnoses where a false positive can lead to unnecessary treatments or interventions.

Type 2 Error (False Negative): Type 2 error occurs when a null hypothesis is incorrectly accepted, indicating a false negative result. In machine learning, it means incorrectly classifying a positive instance as negative. It is similar to a false negative error mentioned earlier. Type 2 errors are significant when minimizing false negatives is essential, such as in medical diagnoses where a false negative can result in a missed diagnosis or delayed treatment.

Cross-validation

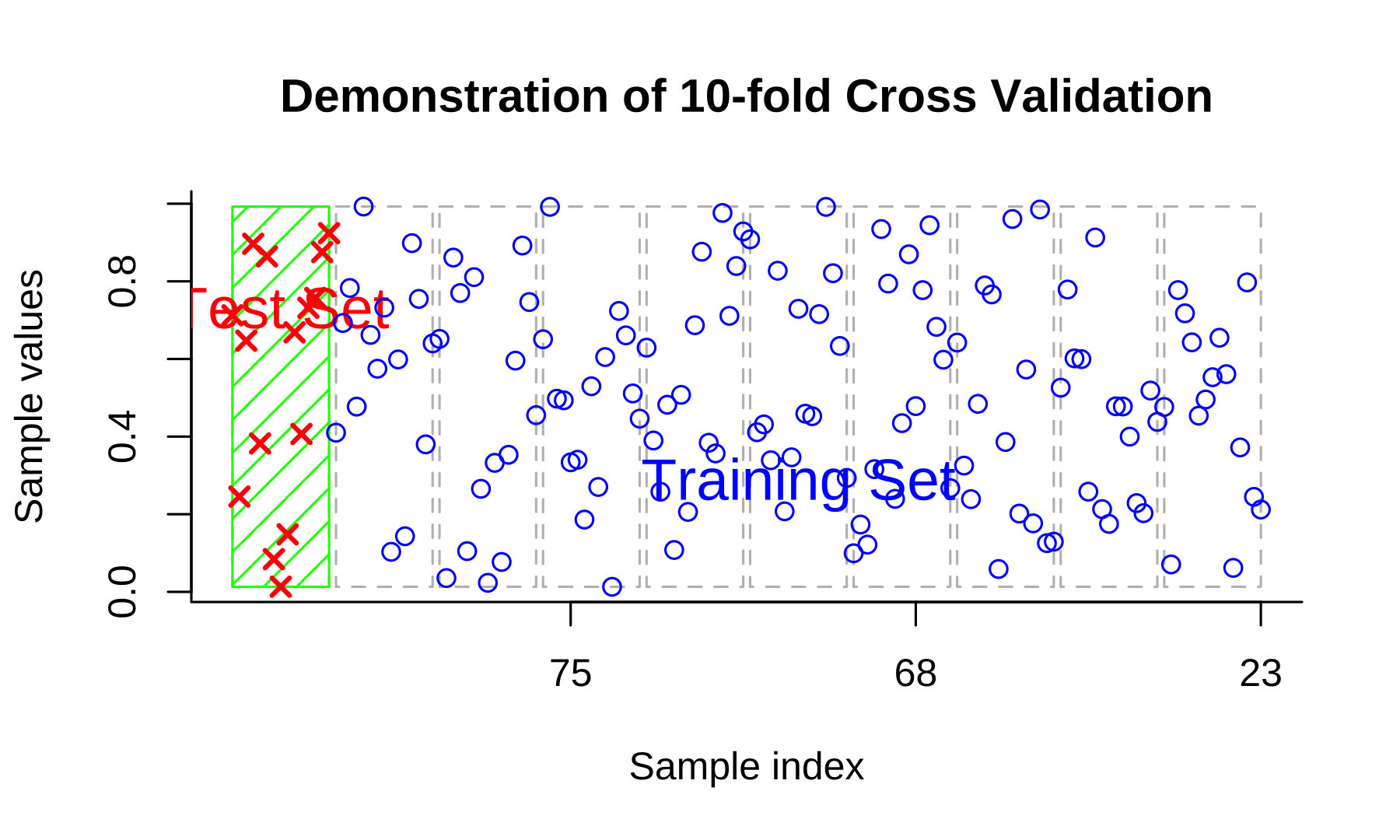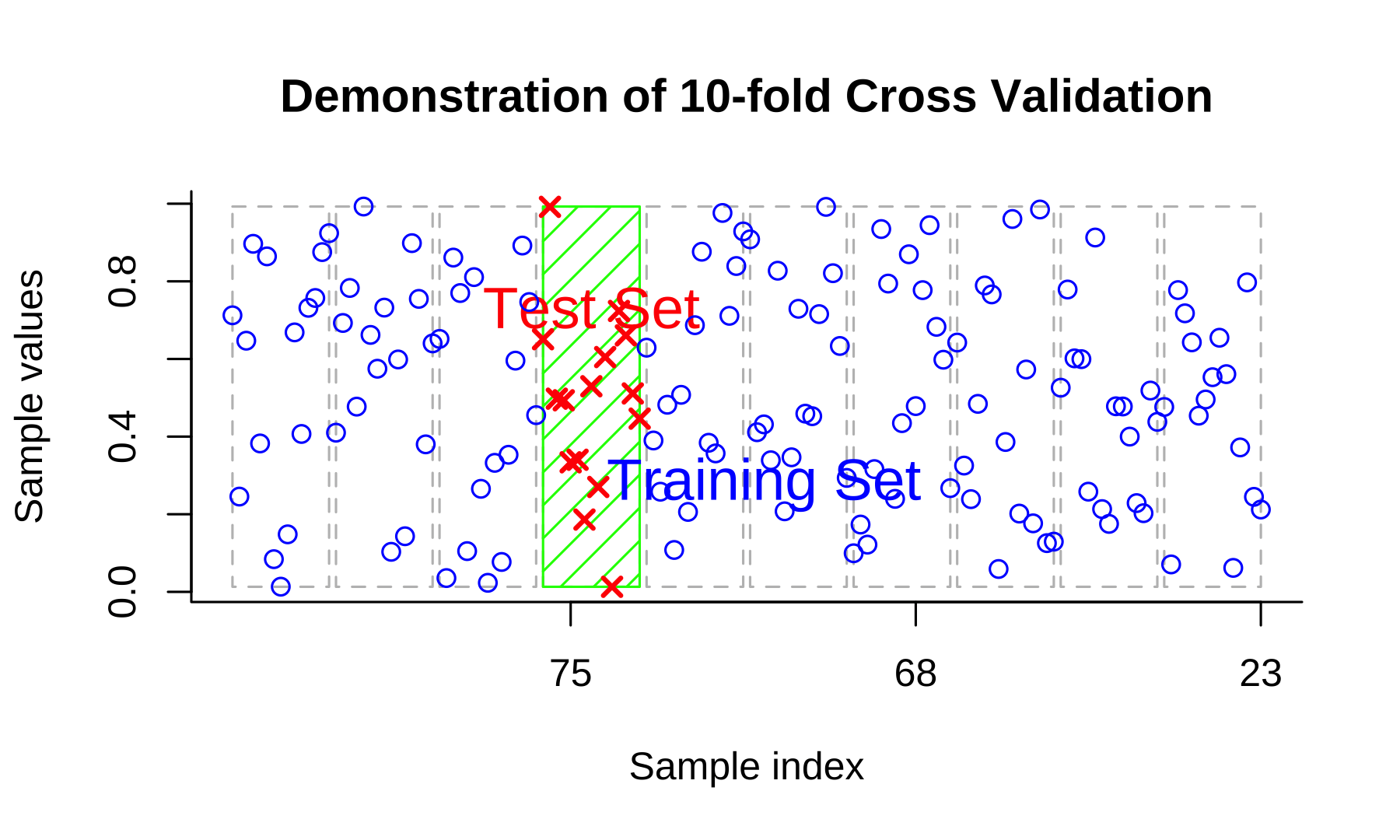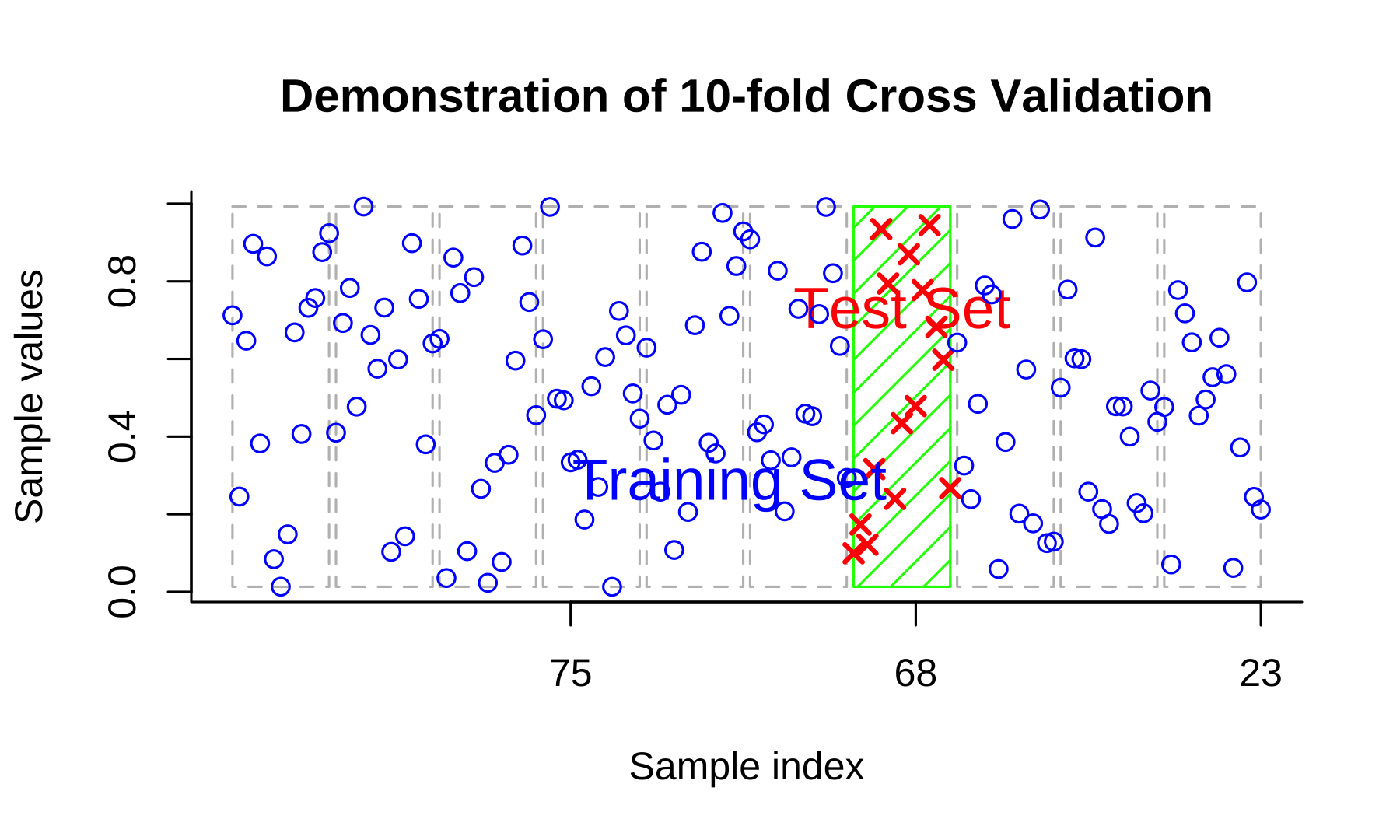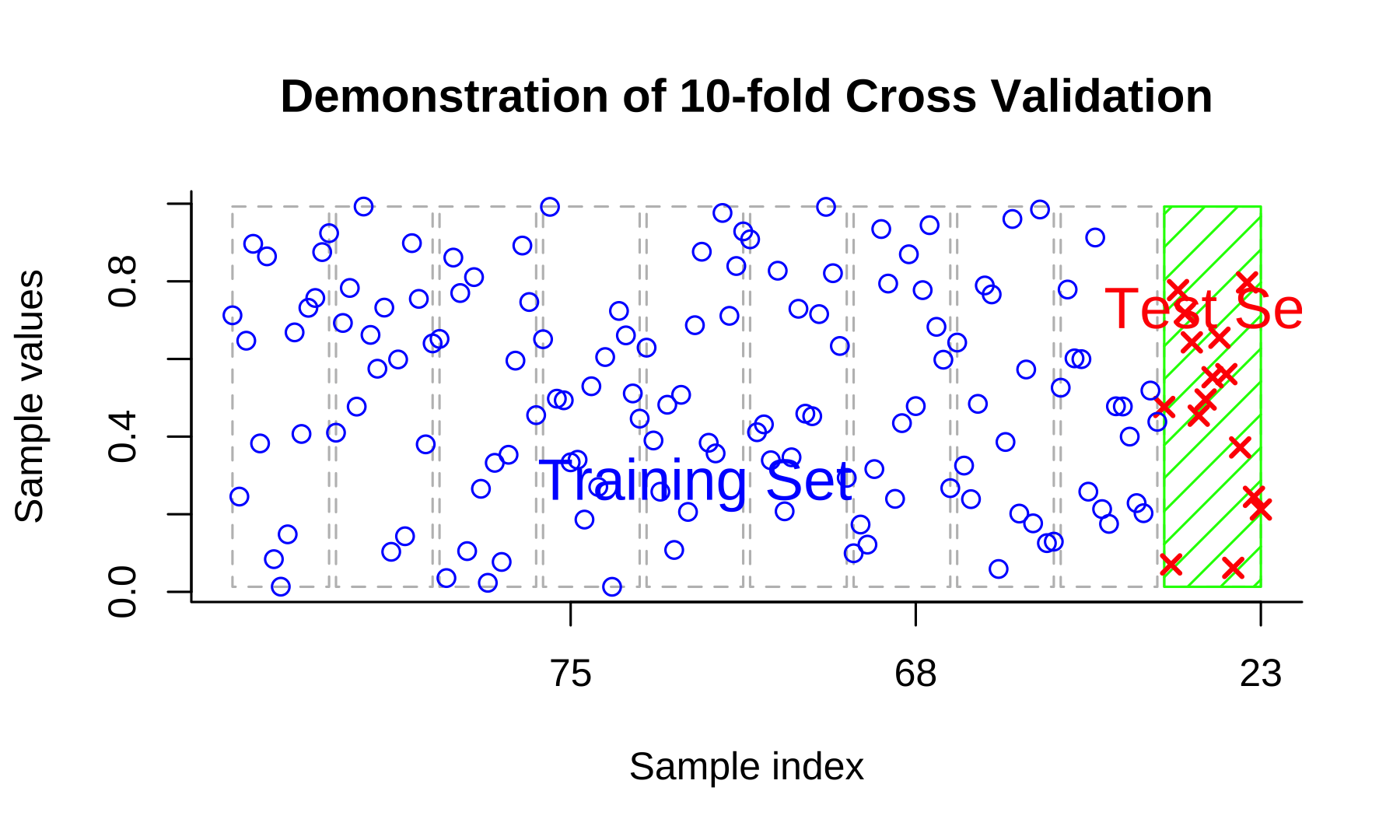
Resource: Cross-Validation Review

Cross-validation is a technique in machine learning used to assess the performance and generalization ability of a model. It involves dividing the available dataset into multiple subsets or "folds." The model is trained on a portion of the data (training set) and evaluated on the remaining fold (validation set). This process is repeated multiple times, with each fold serving as the validation set in turn. The performance metrics obtained from each iteration are then averaged to provide a more robust estimate of the model's performance.

Cross-validation helps to mitigate the risk of overfitting and provides a more accurate assessment of how well the model will perform on unseen data. Commonly used cross-validation methods include k-fold cross-validation, stratified k-fold cross-validation, and leave-one-out cross-validation. By utilizing cross-validation, researchers and practitioners can make informed decisions about model selection, hyperparameter tuning, and assess the model's performance under different scenarios.